Bacterial cultures

An individual based model has been developed and designed to simulate the growth and behaviour of bacterial populations. The fundamental unit of bacterial life is the bacterial cell. Since our work is an individual based model, we have constructed our simulation code in terms of individual bacterial cells and their behaviour, within a set environment.
We have named INDISIM the simulator devised to implement our models. INDISIM stands for INDividual DIScrete SIMulations, and shares the same philosophy of other individual-based models. It describes bacterial properties, including substrate uptake, metabolism, maintenance, cell division, viability and death at individual level. INDISIM is discrete in space and time, and controls a group of bacterial cells at each time step, using a set of random, time dependent, variables for each bacterium. These variables are used to characterise its position in space, biomass, and state in the cellular reproduction cycle as well as other individual properties. The space where the bacterial population evolves is also discrete. A physical lattice is introduced, subject to the appropriate boundary conditions. The lattice is subdivided into spatial cells (normally squares or cubes) also defined by a set of random, time dependent, variables. These variables may include concentrations of different types of particles, nutrient and residual products. We use of random variables for the characterisation of individual rules and the characterisation of individual properties of a bacterial cell and a spatial cell, as well as the random updating of individual rules. The stochasticity of the simulations implies variability of individual behaviour. The time evolution of the system is divided into equal intervals that we identify with program steps.
The environment where the bacterial population evolves may be a liquid or a solid. We specifically consider the evolution of a bacterial population over a period of time in a specific environment occupying a two - or three - dimensional spatial grid. The size, shape and composition of the physical lattice also affect the environmental conditions. The properties of the media are modelled by using simple physical relations. We can incorporate into our code the entrance (exit) of nutrient particles from outside (inside) the system, or other agents external to it.

INDISIM has been used to study:

The biomass distribution of the bacterial population growing in optimal conditions and what happen when the conditions are not optimal.
The relationship between the rate of growth of a bacterial population to the nutrient concentration and temperature.
Metabolic oscillations in a batch bacterial system, the temporal evolutions of heat dissipation and pressure of a population of Escherichia coli in a batch culture.

Fig.2: Escherichia coli bacteria from http://aquat1.ifas.ufl.edu/guide/bacteria.html

The influence of the geometry of bacterial cells in yoghurt processing, Streptococcus thermophilus as spherical cells and Lactobacillus bulgaricus as cylindrical cells, as well as their interaction."

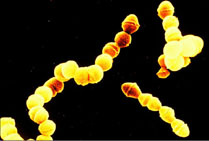
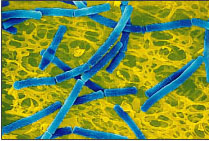
Fig.3:Which is the Lactobacillus? The Streptococcus? The starter culture for
most yogurt production is a symbiotic blend of Streptococcus thermophilus
(ST) and Lactobacillus bulgaricus (LB). These bacteria use lactic-acid
fermentation to produce energy for growth; they lack a respiratory
metabolism. Although these bacteria can grow independantly, the rate of acid
production is much higher when used together than either of the two
organisms grown individually. ST grows faster and produces acid. The acid
stimulates LB growth. On the other hand, the proteolytic activity of LB
produces stimulatory peptides and amino acids for use by ST. These
microorganisms are ultimately responsible for the formation of typical
yogurt flavor and texture. From http://smccd.net/accounts/case/biol215/indmic.html

The qualitative trends of pattern formation that appear during the growth of Bacillus subtilis on an agar plate under different initial conditions of nutrient concentration and different amount of agar.

Fig.4:Bacteria colony in an agar suspension from http://www.sciencehound.com/science_project_community/node/5333

Fig.5:The simulated growth of a DLA-like colony pattern. A simulated "point"
inoculum was placed at the centre of the lattice with a relatively low,
uniformly distributed, initial nutrient concentration input Sx,y(0) = 200 ,
and a microscopic diffusion D = 0.05, which is also relatively small.
Figures (a), (b), and (c) show different stages in the growth of the
bacterial colony. The squares and circles identify branches which have
stopped growing (Ginovart et al., Physica A 305 (2002) 604 - 618)

Lag phase

The lag phase in bacterial cultures is of great importance in food microbiology. It is an area of study in predictive microbiology, which attempts to understand the microscopic causes of the lag phase, so as to predict the evolution of a microbial culture under given conditions. In consequence, the cell mechanisms of growth and division, as well as the cell adaptation mechanisms in a new environment, must be understood.

Mathematical descriptions of the lag phase already exist. Some of them (Baranyi and Roberts, 1994; Hills and Wright, 1994; McKellar, 1997) are based on a dynamic description of growth, bymeans of differential equations. Later models introduced stochastic treatments (Buchanan et al., 1997; McKellar, 2001; Baranyi, 2002), with more realistic features. Recent studies have also tried to relate individual cells' lag times with population lag time (Wu et al., 2000; Métris et al., 2003; Kutalik et al., 2005). All these models have been used to study different aspects of the lag phase, such as the influence of the medium (temperature, pH, etc.) and the initial conditions of the inoculum. Nevertheless, in order to develop existing models, more knowledge of the underlying biological mechanisms causing the lag must be incorporated, which requires a more complete knowledge of the behaviour of individual cells (Buchanan et al., 1997; McKellar et al., 2002). Modelling and simulation at an individual level are good tools to explore the biological mechanisms of the bacteria. This is also a good way to study the mechanistic constraints of the individual cells in depth, something not taken into account by the aforementioned mathematical and stochastic treatments (Swinnen, 2004).

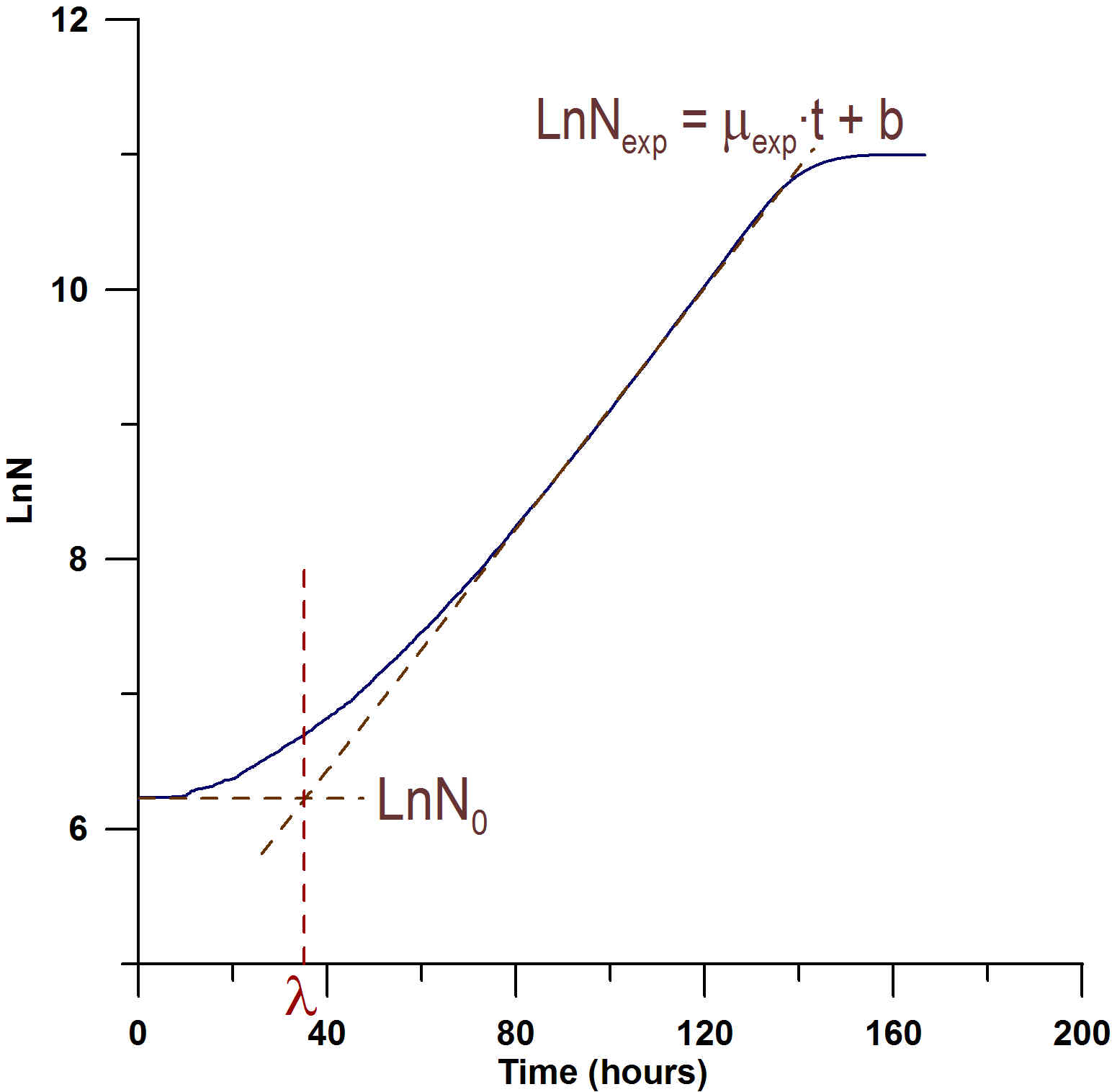
Fig. 1: Lag parameter calculus by means of the geometrical method.

Furthermore, experimental techniques have been developed to obtain results from individual cells (Smelt et al., 2002, Elfwing et al., 2004). Modelling and simulation at the individual level can be useful to understand the results obtained. Moreover, this method can be used to design new experiments to improve understanding of individual and population behaviour.
For these reasons, it seems to be appropriate to introduce Individual-based Modelling (IbM) into this research field (Kreft et al., 1998; Grimm et al., 1999; 2002a; McKellar and Knight, 2000; Swinnen et al., 2004). The principles of IbM are explained by Bernaerts et al. (2003). Actually, two papers which use an IbM approach to study microbial lag have recently been published (Dens et al., 2005a; Dens et al., 2005b). However, these studies concern a specific system: the lag phenomena induced by temperature shifts in Escherichia coli cultures.

Our group has developed, coded and used the IbM simulator we named INDISIM (INDividual DIScret SIMulation) (Ginovart et al., 2002a). INDISIM permits the study of the evolution of a bacterial culture. It is based on the individual behaviour of the bacteria, over a period of time in a specific environment, and subject to appropriate boundary conditions, in which space and time are discrete.

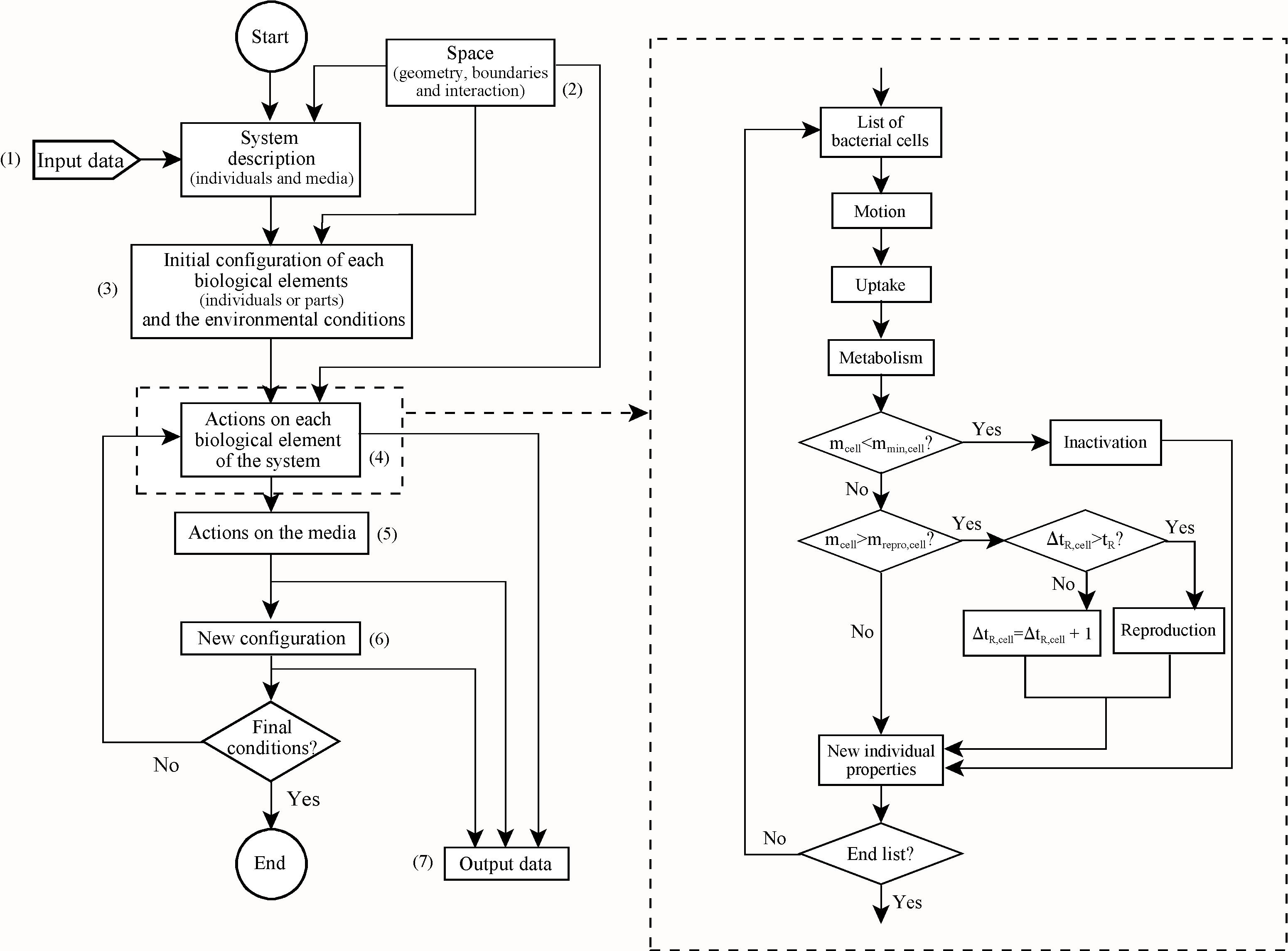
Fig. 2: Flow chart of the computer code (INDISIM). Note that there are three main parts: a) the initialisation, where the input parameters are read (1), the spatial structure is defined according to the cellular method and periodic boundary conditions (Allen and Tildesley, 1987) (2) and the environment and initial population are configured (3); b) the main loop, where at each time step the actions described on the right and detailed in Appendix B are taken for every bacteria of the medium (4), the actions over the medium (nutrient diffusion or redistribution, enzyme action over polymers, extracellular enzyme diffusion, etc.) are done (5) and a new configuration is obtained (6); and c) the final part of the code, where the necessary calculations are made to obtain the results (7).

CLICK HERE FOR A LAG PHASE SIMULATION DEMO